Question

The motion of a particle connected to a spring is described by x = 10 sin (pi*t). At

what time (in s) is the potential energy equal to the kinetic energy?

a. 0
b. 0.25
c. 0.50
d. 0.79
e. 1.0

Answer 1

To solve this problem we will first apply the principle of energy conservation, for which the elastic potential energy must be the same as the elastic kinetic energy of the simple harmonic movement of the system.

From this conservation it will be possible to find in total terms the total displacement of the system and thus replace it in the given function to find the time.

The potential energy stored would be

`PE= (1)/(2) kx^2`

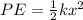
The kinetic energy would be

`KE = (1)/(2)m\omega (A^2-x^2)`

Here,

`A = 10m`

`\omega = \pi rad/s`

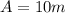
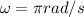
Now assuming the planned conservation of energy

`PE = KE`

`(1)/(2)kx^2 =(1)/(2) m\omega^2 (A^2-x^2)`

`(1)/(2)kx^2 = (1)/(2) m(x(k)/(m))(A^2-x^2)`

`x^2 = A^2 -x^2`

`2x^2 = A^2`

`x = (A)/(√(2))`

`x = (10)/(√(2))`

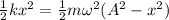
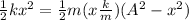
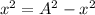
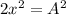
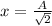
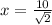
So now using the equation previously given to describe the motion of the particle we have to

`(10)/(√(2)) = 10 sin(xt)`

`(1)/(√(2)) = sin (xt)`

`sin^(-1) ((1)/(√(2)) ) = \pi t`

`(\pi)/(4) = \pi t`

`t = (1)/(4)s= 0.25s`

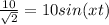
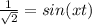
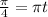
Therefore the correct option is B.

Answer 2

0.25 (Option b is correct )

Step-by-step explanation:

For Spring:

Potential Energy= P.E=
`(1)/(2)kx^2`

Kinetic energy=K.E=
`(1)/(2)m\omega(A^2-x^2)`

Where:

x is the displacement

A is the Amplitude (Maximum Displacement)

P.E=K.E

`(1)/(2)kx^2=(1)/(2)m\omega(A^2-x^2)`

We are given that:

`x=10 sin (\pi*t)` Equation (1)

From this:

A=10

ω=k/m

Putting in above equation:

`(1)/(2)kx^2=(1)/(2)m*(k)/(m) (10^2-x^2)`

Final Equation will become:

`x^2=10^2-x^2\\2x^2=10^2\\x=(10)/(√(2) )`

Putt value of x in Equation (1)

`(10)/(√(2) ) =10sin(\pi*t)\\(1)/(√(2) ) =sin(\pi*t)\\Since\\\ Sin((\pi)/(4))=(1)/(√(2) ) \\ Sin((\pi)/(4))=sin(\pi*t)\\t=(1)/(4)\\t=0.25`

Option b is correct