Question

A submarine has a mass of 10,000 metric tons. how much water must be displaced for the sub to be in equilibrium just below the ocean surface?

Answer 1

To solve this problem we will apply the concepts related to the Pascal principle for which the balance of Forces between the Buoyancy Force and the body weight is defined.

We define the weight of the body in the international system as

`M = 10\text{metric tones}(\frac{1000kg}{1\text{metric tones}})`

`M = 1*10^7kg`

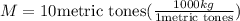
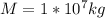
At the same time, the force caused by seawater as

`W = mg = \rho Vg`

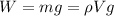
Note: Remember that the definition of density tells us that
`\rho = (m)/(V)`

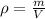
Here,

m = mass

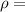`\rho =`Density

V = Volume

g = Gravity

As a reaction force is the buoyancy force then

`F_B = \rho Vg`

`F_B = (1.03*10^3kg/m^3)V (9.8)`

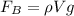
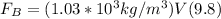
If the body is in balance then the balance of forces tells us that

`\sum F = 0`

`F_B -Mg=0`

`F_B = Mg`

`(1.10*10^3) V(9.8)=1*10^7kg`

`V = (1*10^7)/(1.03*10^3)`

`V = 0.9708*10^4m^3`

`V = 9.704*10^3m^3`

`V = 9708m^3`

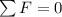
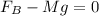
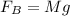
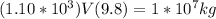
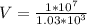
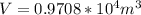
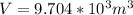
Therefore the total water displaced is
`V = 9708m^3`