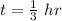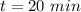Question

A woman can row a boat at 4.0 mph is still water.

1. If she is crossing a river where the current is 2.0 mph, in what direction must her boat be headed if she wants to reach a point directly opposite her starting point?
2. If the river is 4.0 mi wide, how long will it take her to cross the river?

Answer 1

1)
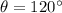`\theta=120^(\circ)` from the positive x-axis.

2)
`t=20\ min`

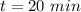
Step-by-step explanation:

Given:

speed of rowing in still water,
`v=4\ mph`

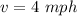
1)

speed of water stream,
`v_s=2\ mph`

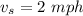
we know that the direction of resultant of the two vectors is given by:

`tan\ \beta=(v.sin\ \theta)/(v_s+v.cos\ \theta)`

where:

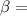`\beta=`the angle of resultant vector from the positive x-axis.

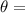`\theta =` angle between the given vectors

When the rower wants to reach at the opposite end then:

`\beta =90^(\circ)`

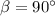
so,

`tan\ 90^(\circ)=(v.sin\ \theta)/(v_s+v.cos\ \theta)`

`\Rightarrow v_s+v.cos\ \theta=0`

`2+4* cos\ \theta=0`

`cos\ \theta=-(1)/(2)`

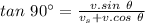
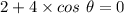
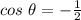
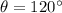`\theta=120^(\circ)` from the positive x-axis.

2)

Now the resultant velocity of rowing in the stream:

`v_r=√(v^2+v_s^2+2* v.v_s.cos\ \theta)`

`v_r=√(4^2+2^2+2* 4* 2* cos\ 120)`

`v_r=12\ mph`

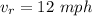
Therefore time taken to cross a 4 miles wide river:

`t=(4)/(12)`

`t=(1)/(3)\ hr`

`t=20\ min`