Question

There are 2 black balls, one red ball and one green ball, identical in shape and size. How many different linear arrangements can be generated by arranging these balls?

Answer 1

Answer: The number of different linear arrangements can be generated by arranging these balls is 12.

Explanation:

The number of ways to arrange n things in a line where a things are like and b things are like is
`(n!)/(a!\ b!\ ....)`

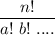
Given : There are 2 black balls, one red ball and one green ball, identical in shape and size.

Total balls = 2+1+1=4

Here 2 black balls are alike.

So , the number of different linear arrangements can be generated by arranging these balls would be
`(4!)/(2!)=(4*3*2!)/(2!)=12`

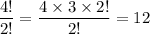
Hence, the number of different linear arrangements can be generated by arranging these balls is 12.