Answer:
Explanation:
The given question is incomplete; please find the complete question enclosed as an attachment.
Area of the material by which silo is to be build = 1000 square ft
a). Since Surface area of the silo is represented by the formula
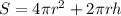
By replacing S = 1000
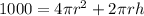
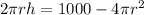
![h=(1)/(2 \pi r)[1000-4\pi r^(2)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/dz6nn0qef5qkor0r2mskmvyz5v8doaexur.png)
b). Expression representing the volume is given by
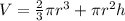
By replacing the value of h from option (a) to the option (b).
![V=(2)/(3)\pi r^(3)+\pi r^(2)[((1)/(2\pi r))(1000-4\pi r^(2))]](https://img.qammunity.org/2021/formulas/mathematics/high-school/x1xc74is69w37e08ujbmzyrk408rk1ikdz.png)
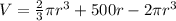

c). For the maximum volume of silo we will find the derivative of V and equate it to zero.
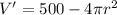 = 0
= 0
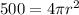
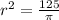

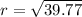
r = 6.31 feet
For r = 6.31 ft,
![h=[(500)/(\pi r)-2r]](https://img.qammunity.org/2021/formulas/mathematics/high-school/mix0g10hh21iyaianwsvdty7wpon2bpa7q.png)
![h=[(500)/(\pi (6.31))-2(6.31)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/zknxx5lx5kcxct9sc2obp7pdt1bqr1kbsf.png)
![h=[25.21-12.62]](https://img.qammunity.org/2021/formulas/mathematics/high-school/q7cbl30ge23rsxzy7xyz7ejp6us7ki59j6.png)
h = 12.59 ft
Therefore, silo will have 6.31 ft height and 12.59 ft height for the maximum volume.