Question

The Hubble Space Telescope orbits 600 km above Earth's surface. Earth's radius is about 6370 km. Use the Pythagorean Theorem to find the distance x from the telescope to Earth's horizon. Round your answer to the nearest ten kilometers.

Answer 1

To solve this problem we will apply the concept given by Pythagoras in the description of the lengths of the legs of a rectangular triangle and if equality against the square of the hypotenuse, that is

`a^2+b^2=c^2`

Here,

a, b = Legs of a triangle

c = Hypotenuse

According to the attached chart then we would have to

`a=x\\b = 6370km\\c = 600+6370km = 6970km`

Substituting the given the lengths into the Pythagorean Theorem.

`a^2+b^2 = c^2 \\x^2 +(6370)^2 = (6970)^2\\x = 2829.13km \approx 2830km`

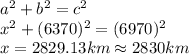
Therefore the distance x is 2830km.