Question

Use the following information to answer the next nine exercises: The population parameters below describe the full-time equivalent number of students (FTES) each year at Lake Tahoe Community College from 1976–1977 through 2004–2005.

• μ = 1000 FTES
• median = 1,014 FTES
• σ = 474 FTES
• first quartile = 528.5 FTES
• third quartile = 1,447.5 FTES
• n = 29 years

Additional Information: The population FTES for 2005—2006 through 2010—2011 was given in an updated report. The data are reported here.

Year: 2005-06 2006-07 2007-08 2008-09 2009-10 2010-11
Total FTES: 1585 1690 1735 1935 2021 1890

Compare the IQR for the FTES for 1976—77 through 2004—2005 with the IQR for the FTES for 2005-2006 through 2010— 2011. Why do you suppose the IQRs are so different?

Answer 1

Explanation:

Hello!

Complete Question:

The population parameters below describe the full-time equivalent number of students (FTES) each year at Lake Tahoe Community College from 1976–1977 through 2004–2005.

• μ = 1000 FTES

• median = 1014 FTES

• σ = 474 FTES

• first quartile = 528.5 FTES

• third quartile = 1447.5 FTES

• n = 29 years

1) A sample of 11 years is taken. About how many are expected to have FTES of 1014 or above?

Assuming the median value is the same as de one given above, Me= 1044, it means that 50% of the sample is below this number of FTES and the other 50% is above.

To calculate the year above you have to calculate the median position (Pos Me) for the sample n= 11

Pos Me= (n+1)/2= (11+2)/2= 6

Answer: 6 years have FTES of 1014 or above.

2) 75% of all years have FTES

Quantiles are position measurements that separate the sample in equal-sized subgroups.

The first quantile C₁ leaves 25% of the sample below it and 75% of the sample above.

The second Quantile C₂ (Median) separates the sample in exactly 50%

The third Quantile C₃ leaves 75% of the sample below and 25% of the sample above.

a. At or below

This question refers to the third Quantile (75% of the sample below)

C₃= 1447.5 FTES

b. At or above

This question refers to the first Quantile (75% of the sample above)

C₁= 528.5 FTES

3) The population standard deviation

The standard deviation is symbolized with the greek letter sigma (σ)

σ= 474 FTES

4) What percent of the FTES was from 528.5 to 1447.5? How do you know?

528.5 corresponds to the first Quantile and 1447.5 corresponds to the third Quantile.

By definition the Interquartile range (IQR), also called middle 50%, is a measure of dispersion, defined as the difference between the C₃ and C₁ and comprises 50% of the sample.

This means that between 528.5 and 1447.5 is 50% of the FTES.

5) What is the IQR? What does the IQR represent?

Defined in 4)

C₃ - C₁= 1447.5 - 528.5= 919

6) How many standard deviations away from the mean is the median?

The mean (μ) is 1000 FTES

The meadian (Me) is 1014 FTES

Their difference is (Module): Iμ - MeI= I1000 - 1014I= I-14I= 14

Using rule of three:

`(474)/(1) = (14)/(x)`

`x= (14*1)/(474) = 0.029`

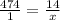
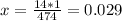
Then the Median is 0.029σ away from the mean.

Additional Information: The population FTES for 2005—2006 through 2010—2011 was given in an updated report. The data are reported here.

Year: 2005-06 2006-07 2007-08 2008-09 2009-10 2010-11

Total FTES: 1585 1690 1735 1935 2021 1890

7) Calculate the mean, median, standard deviation, first quartile, the third quartile, and the IQR. Round to one decimal place.

You have the amount of FTES per year for n= 6 years.

The variable is discrete and you have the observed number of students per year, using the following formulas you can calculate the asked measurements.

Mean:

(∑x)/n = 10856/6= 1809.3 FTES

Median:

Position (n+1)/2 = (6+1)/2 = 3.5

Now you list the observed values in increasing order:

Position 1 2 3 4 5 6

Observed frequency 1585 1690 1735 1890 1935 2021

Since the median is in position 3.5 you have to calculate the midpoint between positions 3 and 4 to know its value:

Position 3: 1735

Position 4: 1890

Me=
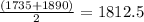`((1735+1890))/(2) = 1812.5` FTES

Standard deviation

S²=
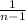`(1)/(n-1)`[∑x²-((∑x)²/n )]

S²=
`(1)/(5)[19779316-((10856)^2)/(6) ]`

S²= 27438.67 FTES²

S= 165.645 ≈ 165.65 ≈ 165.7 FTES

First Quantile

Position: Pos Me - (n*1/4) = 3.5 - (6*1/4) = 2

C₁= 1690 FTES

Third Quantile

Position: Pos Me + (n*1/4) = 3.5 + (6*1/4) = 5

C₃= 1935 FTES

IQR= C₃ - C₁ = 1935 - 1690= 245 FTES

8) Construct a boxplot for the FTES for 2005 - 2006 through 2010 - 2011 and a boxplot for the FTES for 1976-1977 through 2004-2005.

Attached.

9) Compare the IQR for the FTES for 1976—77 through 2004—2005 with the IQR for the FTES for 2005-2006 through 2010— 2011. Why do you suppose the IQRs are so different?

Sample 1:

IQR for the FTES 1976—77 through 2004—2005= 919 FTES

Number of years 29

Sample 2

IQR for the FTES for 2005-2006 through 2010— 2011= 245 FTES

Number of years 6

The main reason that the IQR of sample 1 is larger than the IQR of sample 2 is that the first sample covers a larger period.

I hope it helps!