Question

a password to a certain database consists of digits that cannot be repeated. if the password is known to consist of at least 8 digits and it takes 12 seconds to try one combination, what is the amount of time, in minutes, necessary to guarantee access to the database

Answer 1

`(10!)/(2)mins`

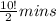
Step-by-step explanation:

12 seconds to try one combination will be equivalent to
`(1)/(12)* 60 = (1)/(5) \ mins`

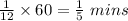
Password contain at least 8 digit i.e. password can contain 8, 9, 10 digit.

Password cannot contain more than 10 digit because it will give room for repetition which it is clearly stated that digit cannot be repeated.

Possible digit that can be used: 9,8,7,6,5,4,3,2,1,0.

Total number of passwords combination possible for each position in 8 digit.

1st position = 10, 2nd position = 9, 3rd position = 8, 4th position = 7, 5th position = 6, 6th position = 5, 7th position = 4, 8th position = 3. Total number of passwords combination possible in 8 digit is equivalent to
`(10!)/(2)`.

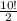Total number of passwords combination possible for each position in 9 digit.

1st position = 10, 2nd position = 9, 3rd position = 8, 4th position = 7, 5th position = 6, 6th position = 5, 7th position = 4, 8th position = 3, 9th position = 2. Total number of passwords combination possible in 9 digit is equivalent to
`(10!)/(1)`.

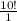Total number of passwords combination possible for each position in 10 digit.

1st position = 10, 2nd position = 9, 3rd position = 8, 4th position = 7, 5th position = 6, 6th position = 5, 7th position = 4, 8th position = 3, 9th position = 2, 10th position = 1. Total number of passwords combination possible in 10 digit is equivalent to 10!.

Adding them up and multiplying by
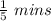`(1)/(5) \ mins` to get the total number of time needed to guarantee access to database =
`[(10!)/(2)*\ (10!)/(1) * 10!] (1)/(5)\ mins = (10!)/(2)`