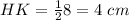Question

GJ is a midsegment of triangle DEF, and HK is a midsegment of triangle GFJ. What is the length of HK?

A) 2.25 centimeters
B) 4 centimeters
C) 7.5 centimeters
D) 9 centimeters.

Answer 1

Option B) 4 centimeters

Explanation:

see the attached figure to better understand the problem

step 1

Find the value of n

we know that

a) GJ is a midsegment of triangle DEF

then

G is the midpoint segment DF and J is the midpoint segment EF

DG=GF and EJ=JF

b) HK is a midsegment of triangle GFJ

then

H is the midpoint segment GF and K is the midpoint segment JF

GH=HF and JK=KF

In this problem we have

HF=7 cm

so

GH=7 cm

GF=GH+HF ----> by addition segment postulate

GF=7+7=14 cm

Remember that

DG=GF

substitute the given values

`2n-1=14`

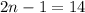
solve for n

`2n=14+1`

`2n=15`

`n=7.5\ cm`

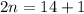
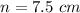
step 2

Find the length of GJ

we know that

The Midpoint Theorem states that the segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side

so

`GJ=(1)/(2)DE`

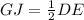
we have

`GE=2n+1=2(7.5)+1=16\ cm`

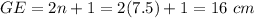
substitute

`GJ=(1)/(2)16=8\ cm`

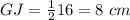
step 3

Find the length of HK

we have that

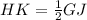`HK=(1)/(2)GJ` ----> by the midpoint theorem

we have

`GJ=8\ cm`

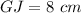
substitute

`HK=(1)/(2)8=4\ cm`