Question

A jar contains n nickels and d dimes. There are 26 coins in the jar, and the total value of the coins is $1.80. How many nickels and how many dimes are in the jar?

Answer 1

There are 16 nickels and 10 dimes in the jar.

Explanation:

Given:

A jar contains n nickels and d dimes.

There are 26 coins in the jar.

The total value of the coins is $1.80.

Now, to find the number of nickels and dimes in the jar.

As given nickels =
`n.`

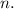
And dimes =
`d.`

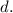
So, the total number of coins:

`n+d=26`

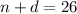
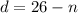`d=26-n`........(1)

The value of a nickel = $0.05.

And the value of a dime = $0.10.

Now, the total value of the coins:

`0.5n+0.10d=1.80`

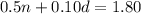
Putting the value of
`d` from equation (1) we get:

⇒
`0.05n+0.10(26-n)=1.80`

⇒
`0.05n+2.6-0.10n=1.80`

⇒
`2.6-0.05n=1.80`

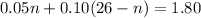
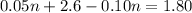
Subtracting both sides by 2.6 we get:

⇒
`-0.05n=-0.80`

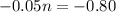
Dividing both sides by -0.05 we get:

⇒
`n=16.`

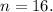
So, the number of nickels = 16.

Now, to get the number of dimes we put the value of
`n` in equation (1):

`d=26-n`

⇒
`d=26-16`

⇒
`d=10`

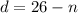
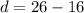
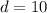
Thus, the number of dimes = 10.

Therefore, there are 16 nickels and 10 dimes in the jar.