Question

Find the value of x in each case. Give reasons to justify your solutions! N ∈ KO

Answer 1

x = 30 degrees

Explanation:

;)

Answer 2

x =30°

Explanation:

Step 1: To find
`\angle \mathrm{KNL}`.

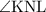Given N ∈ KO, where KO is a line.

Sum of the adjacent angles in a straight line is 180°.

`\Rightarrow \angle \mathrm{KNL}+\angle \mathrm{LNM}+\angle \mathrm{MNO}=180^(\circ)`

`\Rightarrow \angle \mathrm{KNL}+45^(\circ)+105^(\circ)=180^(\circ)`

`\Rightarrow \angle \mathrm{KNL}+150^(\circ)=180^(\circ)`

`\Rightarrow \angle \mathrm{KNL}=180^(\circ)-150^(\circ)`

`\Rightarrow \angle \mathrm{KNL}=30^(\circ)`

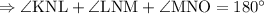
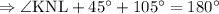
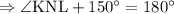
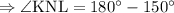
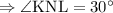
Step 2: To find
`\angle \mathrm{NLK}`.

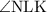Sum of the adjacent angles in a straight line is 180°.

Given
`\angle \mathrm{NLM}=90^(\circ)`

`\Rightarrow \angle \mathrm{NLM}+\angle \mathrm{NLK}=180^(\circ)`

`\Rightarrow \angle \mathrm{NLK}=180^(\circ)-90^(\circ)`

`\Rightarrow \angle \mathrm{NLK}=90^(\circ)`

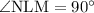
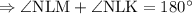
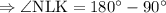
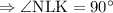
Step 3: To find x.

Sum of the interior angles in a triangle is 180°.

Let us take the triangle NLK.

`\Rightarrow \angle \mathrm{KNL}+\angle \mathrm{NLK}+\angle \mathrm{LKN}=180^(\circ)`

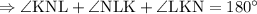
⇒ 30° + 90° + 2x = 180°

⇒ 2x = 180° – 30° – 90°

⇒ 2x = 60°

⇒ x = 30°

Hence, x = 30°.