Answer:
The graph is shown below.
Explanation:
Given:
The relationship between the variables 'x' and 'y' is proportional relationship.
A proportional relationship is of the form:
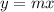
Where 'm' is called the constant of proportionality and also the slope of the line
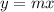
Now, it is given that 'y' is one-half of the value of 'x'. Framing it in equation form, we get:
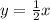
So, the slope of the line is

Slope is nothing but rise over run. Run is parallel the x-axis and rise is parallel to the y-axis.
Now, a proportional relationship always passes through the origin.
So, in order to get slope equal to one-half, we need to move 2 units along the x-axis from the origin and then 1 unit parallel to y-axis to get to the next point. The point is (2, 1).
Now, we draw a line passing through the origin and (2, 1) which is the required of the given proportional relationship.