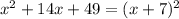Answer:
Divide the b parameter by 2 and rewrite it as the square of a binomial inserting the x, and the c as the half of b.
.
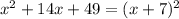
Explanation:
1) Every perfect square trinomial can be written as the square of a binomial. For instance:
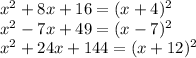
2) Firstly let's complete the square
2a. Find "c", the constant term by dividing "b"
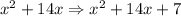
2b. Square it

3) Since we completed the square, then to write that trinomial as the square of a binomial :
Divide the b parameter by 2 and rewrite it as the square of a binomial inserting the x, and the c as the half of b.
.