Answer:
A.
![(\sqrt[3]{125})^9\ and\ (125)^{(9)/(3)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/j3dylzy8x6osc8nqwkax8be4lw59pu2scm.png)
D.
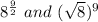
Explanation:
Equivalent expressions are those expressions that simplify to same form.
Now, let us check each of the given options.
Option A:
![(\sqrt[3]{125})^9\ and\ (125)^{(9)/(3)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/j3dylzy8x6osc8nqwkax8be4lw59pu2scm.png)
We know that,
![\sqrt[n]{x} =x^{(1)/(n)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/jm768bjepgtuz2fktj03nc6o37fb41iqjk.png)
Therefore,
![\sqrt[3]{125} =(125)^{(1)/(3)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/a25no0ns0ldb9hdul5cuhig7odg6z4gtmj.png)
Thus the first expression becomes;
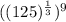
Now, using law of indices
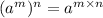 , we get
, we get

Therefore,
![(\sqrt[3]{125})^9\ and\ (125)^{(9)/(3)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/j3dylzy8x6osc8nqwkax8be4lw59pu2scm.png) are equivalent.
are equivalent.
Option B:
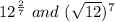
Consider the second expression

We know that,
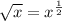
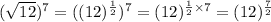
Therefore,
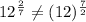 . Hence, the expressions
. Hence, the expressions
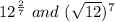 are not equivalent.
are not equivalent.
Option C:
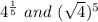
We know that,
![x^{(1)/(n)}=\sqrt[n]{x}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/clzwcozuiwrkxsajfflesk9vs3dd3et8q4.png)
Therefore,
![4^{(1)/(5)}=\sqrt[5]{4}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/9n7mrqgnhc29iwavs4f1ut3msur7hqqm9o.png)
Now,
![\sqrt[5]{4}\\e (\sqrt 4)^5](https://img.qammunity.org/2021/formulas/mathematics/middle-school/5nasb9uprygj6z7wfjirk0a9tqy4n1xmg0.png)
Therefore, the expressions
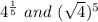 are not equivalent.
are not equivalent.
Option D:

Using law of indices
 , we get
, we get

Now, we know that,

So,
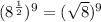
Therefore,
 are equivalent.
are equivalent.