Question

Which of these choices show a pair if equivelent expressions? Chack all that apply

A. (^3√125)^9 and 125^9/3
B. 12^2/7 and (√12)^7
C. 4^1/5 and (√4)^5
D. 8^9/2 and (√8)^9

Answer 1

A.
`(\sqrt[3]{125})^9\ and\ (125)^{(9)/(3)}`

D.
`8^{(9)/(2)}\ and\ (√(8))^9`

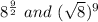
Explanation:

Equivalent expressions are those expressions that simplify to same form.

Now, let us check each of the given options.

Option A:

`(\sqrt[3]{125})^9\ and\ (125)^{(9)/(3)}`

We know that,

`\sqrt[n]{x} =x^{(1)/(n)}`

Therefore,
`\sqrt[3]{125} =(125)^{(1)/(3)}`

Thus the first expression becomes;

`((125)^{(1)/(3)})^9`

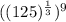
Now, using law of indices
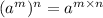`(a^m)^n=a^(m* n)`, we get

`((125)^{(1)/(3)})^9=((125))^{(1)/(3)* 9}=((125))^{(9)/(3)`

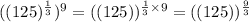
Therefore,
`(\sqrt[3]{125})^9\ and\ (125)^{(9)/(3)}` are equivalent.

Option B:

`12^{(2)/(7)}\ and\ (√(12))^7`

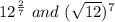
Consider the second expression
`(√(12))^7`

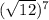
We know that,

`\sqrt x=x^{(1)/(2)}`

`(√(12))^7=((12)^{(1)/(2)})^7=(12)^{(1)/(2)* 7}=(12)^{(7)/(2)}`

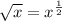
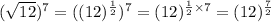
Therefore,
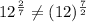`12^{(2)/(7)} \\e (12)^{(7)/(2)}`. Hence, the expressions
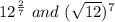`12^{(2)/(7)}\ and\ (√(12))^7` are not equivalent.

Option C:

`4^{(1)/(5)}\ and\ (\sqrt 4)^5`

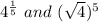
We know that,

`x^{(1)/(n)}=\sqrt[n]{x}`

Therefore,
`4^{(1)/(5)}=\sqrt[5]{4}`

Now,
`\sqrt[5]{4}\\e (\sqrt 4)^5`

Therefore, the expressions
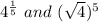`4^{(1)/(5)}\ and\ (\sqrt 4)^5` are not equivalent.

Option D:

`8^{(9)/(2) }\ and\ (\sqrt 8)^9`

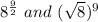
Using law of indices
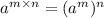`a^(m* n)=(a^m)^n`, we get

`8^{(9)/(2) }=(8^{(1)/(2)})^9`

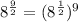
Now, we know that,
`x^{(1)/(2)}=\sqrt x`

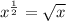
So,
`(8^{(1)/(2)})^9=(\sqrt8)^9`

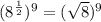
Therefore,
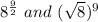`8^{(9)/(2) }\ and\ (\sqrt 8)^9` are equivalent.