To solve this problem we will apply the concepts related to the balance of Forces, the centripetal Force and Newton's second law.
I will also attach a free body diagram that allows a better understanding of the problem.
For there to be a balance between weight and normal strength, these two must be equivalent to the centripetal Force, therefore
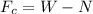
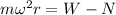
Here,
m = Net mass
 = Angular velocity
= Angular velocity
r = Radius
W = Weight
N = Normal Force

The net mass is equivalent to
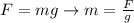
Then,
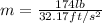
Replacing we have then,
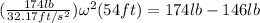
Solving to find the angular velocity we have,
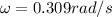
Therefore the angular velocity is 0.309rad/s