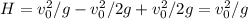Answer:
a)
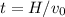
b)
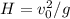
Step-by-step explanation:
Let the first ball throw be the point of reference, we can have following the equation of motion:
1st ball:
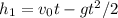
2nd ball:
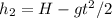
a)When the 2 balls collide they are at the same spot at the same time:
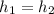
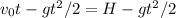
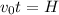
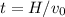
b) The first ball is at its highest point when v = 0. That is
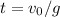
After this time, the 2 balls would have traveled through a distance of
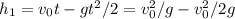
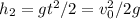
Since
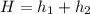 we can solve for H
we can solve for H