Question

Find the equation of the line that is tangent to the circle x2 + y2 = 36 at point (4, -5).

Answer 1

`y = (4)/(5)x-(41)/(5)`

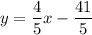
Explanation:

IMPORTANT NOTE:

the radius of the given circle is: 6 with center at origin.

the point (4,-5) is 6.40 units away from the origin (hence, its greater than the radius), so this point doesn't even lie on the circle!

Although we can only use the x-coordinate to find the slope of the tangent that actually touches the circle but that point wont be (4,-5) it'd be some other point (4,a)

But in order to still solve the for the tangent that satisfies (4,-5) and the circle. here's the solution:

To find the equation of the tangent, we need to find the slope of the line at the point (4,-5).

To find the slope of the circle, we need to first differentiate it!

given equation is:

`x^2+y^2=36`

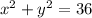
now you can either make y the subject of this equation differentiate then OR you can differentiate it directly. I'm gonna go with the latter since its far easier also we can use both coordinates (4,-5) to find the slope instead of only the x-coordinate.

`(d)/(x)(x^2+y^2)=(d)/(dx)(36)`

`2x+2y(dy)/(dx))=0`

`(dy)/(dx))=(-2x)/(2y)`

`(dy)/(dx))=-(x)/(y)`

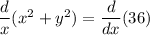
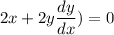
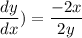
this is the equation of the slope of our circle at any point (x,y). to find the slop at (4,-5). we'll plug in these values.

`(dy)/(dx))=-(4)/(-5)`

`(dy)/(dx))=(4)/(5)`

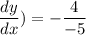
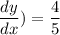
this is also the slope of the tangent at (4,-5), hence,
`m=(4)/(5)`

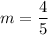
now to find the equation of the tangent: (we'll use the general equation of the line formula)

`(y-y_1) = m(x-x_1)`

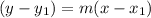
here, m = 4/5 and (x1,y1) =(4,-5)

`(y-(-5)) = (4)/(5)(x-4)`

`y = (4)/(5)x-(4(4))/(5)-5`

`y = (4)/(5)x-(41)/(5)`

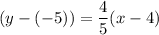
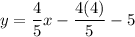
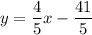
This is the equation of the tangent to the circle!