Answer with Step-by-step explanation:
We are given that
Discriminant, D=
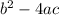
When

Then, the function have two real zeroes.
1.
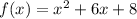
By comparing withe general quadratic equation
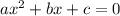
We get a=1,b=6,c=8
Using the discriminant formula
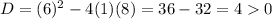
Hence, function have two real zeroes.
2.
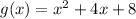
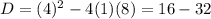
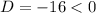
Hence, the function have no two real number zeroes.
3.

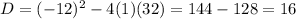
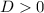
Hence, function have two real zeroes.
4.
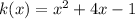
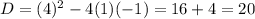
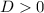
Hence, function have two real zeroes.
5.

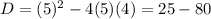
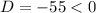
Hence, the function have no two real number zeroes.
6.
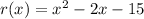
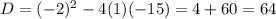
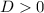
Hence, function have two real zeroes.