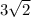Question

What is the absolute value of the complex number Negative 4 minus StartRoot 2 EndRoot i?

StartRoot 14 EndRoot
3 StartRoot 2 EndRoot
14
18

Answer 1

Explanation:

`-4-√(2)i \\ absolute ~value=\sqrt{(-4)^2+(-√(2) )^2} =√(18)=3√(2 )`

Answer 2

Answer : The absolute value of the given complex is,
`3√(2)`

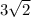
Step-by-step explanation :

As we know that,

The complex number is, a + bi

The absolute value =
`√(a^2+b^2)`

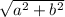
Given :

The complex number
`-4-√(2)i`.

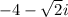For this complex number:

a = -4

b =
`-√(2)`

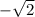
Thus, the absolute value will be:

`√(a^2+b^2)=\sqrt{(-4)^2+(-√(2))^2}=√(16+2)=√(18)=3√(2)`

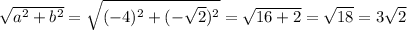
Thus, the absolute value of the given complex is,
`3√(2)`