Answer:
(a) C = +9
(b) C = -9
Explanation:
Given:
The equation to solve is given as:
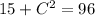
In order to solve this for 'C', we have to isolate 'C' on the left side of the equation.
Adding -15 on both sides, we get:
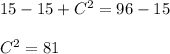
Now, taking square root on both the sides, we get:
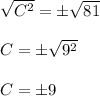
Therefore, there are two values of 'C'.
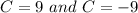
Therefore, options (a) and (b) are correct.