To solve this problem we will apply the concepts related to the thermal efficiency given in an engine of the Carnot cycle. Here we know that efficiency is given under the equation
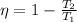
Where,
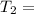 Temperature of Cold Body
Temperature of Cold Body
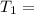 Temperature of Hot Body
Temperature of Hot Body
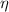 = Efficiency
= Efficiency
According to the statement our values are:
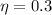
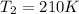
Replacing we have that
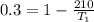
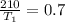
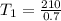
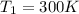
Therefore the temperature of the heat source is 300K