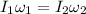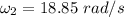Question

A man stands on a platform that is rotating (without friction) with an angular speed of 1.0 rev/s; his arms are outstretched and he holds a brick in each hand. The rotational inertia of the system consisting of the man, bricks, and platform about the central vertical axis of the platform is 6.0 kg·m2. By moving the bricks the man decreases the rotational inertia of the system to 2.0 kg·m2.?

Answer 1

Step-by-step explanation:

Given

`N_1=1 rev/s`

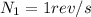
angular velocity
`\omega =2\pi N_1=6.284 rad/s`

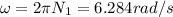
Combined moment of inertia of stool,student and bricks
`=6\ kg.m^2`

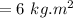
Now student pull off his hands so as to increase its speed to suppose
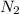`N_2` rev/s

`\omega _2=2\pi N_2`

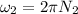
After Pulling off hands so final moment of inertia is

`I_2=2\ kg-m^2`

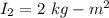
Conserving angular momentum as no external torque is applied

`I_1\omega _1=I_2\omega _2`

`6* 6.284=2* \omega _2`

`\omega _2=18.85\ rad/s`

`N_2=3 rev/s`