Answer:
26
Explanation:
Data provided in the question:
set {1, 2, 3, 5, 11}
Now,
Total number of different choices of a number available = 5
Therefore,
Number of ways to choose 2 distinct numbers= ⁵C₂
Number of ways to choose 3 distinct numbers= ⁵C₃
Number of ways to choose 4 distinct numbers= ⁵C₄
Number of ways to choose 5 distinct numbers= ⁵C₅
therefore,
Total number we can get
= ⁵C₂ + ⁵C₃ + ⁵C₄ + ⁵C₅
=
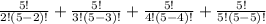
=
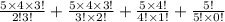
= 10 + 10 + 5 + 1
= 26