Answer:
B) The researcher increases the sample size.
C) The researcher lowers the confidence level.
E) The population standard deviation turns out to be lower than expected.
Explanation:
We are given the following in the question:
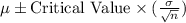
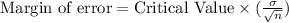
A) The population standard deviation turns out to be higher than expected.
If the standard deviation is higher, the margin of error will increase, hence, the confidence interval will become wider.
B) The researcher increases the sample size.
If the sample size increases, the margin of error decreases, thus, the confidence interval become narrower.
C) The researcher lowers the confidence level.
If the confidence level is decreased, it will decrease the value of test statistic hence, lowering the margin of error.
D) The researcher decreases the sample size.
If the sample size decrease, the margin of error increase, thus, the confidence interval become wider.
E) The population standard deviation turns out to be lower than expected.
If the standard deviation is lower, the margin of error will decrease, hence, the confidence interval will become narrower.
F) The researcher raises the confidence level.
If the confidence level is increases, it will increase the value of test statistic hence, increasing the margin of error.