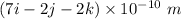Answer:
The distance r is
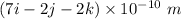
Step-by-step explanation:
Given that,
Origin
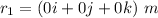
Position of proton
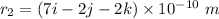
Here, r is the distance from origin to the location of the proton
We need to calculate the distance
Using formula of distance
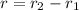
Where, r₁= origin
r₂ = position of proton
Put the value into the formula
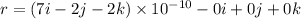
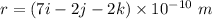
Hence, The distance is