The height of container is 8 feet
Solution:
Let "w" be the width of container
Let "l" be the length of container
Let "h" be the height of container
The width of a container is 5 feet less than its height
Therefore,
width = height - 5
w = h - 5 ------ eqn 1
Its length is 1 foot longer than its height
length = 1 + height
l = 1 + h ---------- eqn 2
The volume of container is given as:
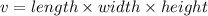
Given that volume of the container is 216 cubic feet
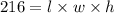
Substitute eqn 1 and eqn 2 in above formula
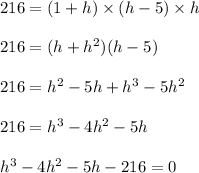
Solve by factoring
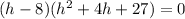
Use the zero factor principle
If ab = 0 then a = 0 or b = 0 ( or both a = 0 and b = 0)
Therefore,
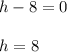
Also,

Solve by quadratic equation formula
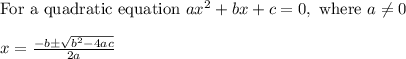
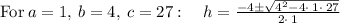
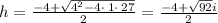
Therefore, on solving we get,
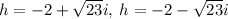
Thus solutions of "h" are:
h = 8
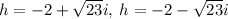
"h" cannot be a imaginary value
Thus the solution is h = 8
Thus the height of container is 8 feet