Question

Identify the roots of the equation and the multiplicities of the roots. HELP ASAP!!

Answer 1

(b)
`(x-5)^2(x+2) = 0` has root 5 of multiplicity 2 and root -2 with multiplicity 1.

Explanation:

Here, the given expression is:
`(x-5)^2(x+2) = 0`

Now, here as we can see from the given expression,

It has 2 roots.

`(x-5)^2(x+2) = 0  \implies (x-5)(x-5)(x+2) = 0`

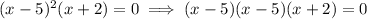
⇒ Either ( x- 5) = 0, or ( x + 2) = 0

⇒ either x = 5 or x = -2

So, x =5 and x = -2 are the ONLY TWO ROOTS of the given expression.

Now, 5 is a root of multiplicity 2 as
`(x-5)^2  = 0`

and, -2 is a root of multiplicity 1 as ( x + 2) = 0

Hence,
`(x-5)^2(x+2) = 0` has root 5 of multiplicity 2 and root -2 with multiplicity 1.