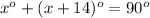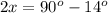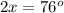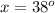Question

Given that ABCD is a rhombus, find the value of x.
(X+14)

Answer 1

option B.
`x=38^o`

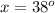
Explanation:

we know that

1) The two diagonals of a rhombus are perpendicular

2) The sum of the interior angles in any triangle must be equal to 180 degrees

Let

O ----> the intersection point of the diagonals of the rhombus

In the right triangle OAD

`x^o+(x+14)^o+90^o=180^o`

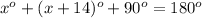
solve for x

`x^o+(x+14)^o=90^o`

`2x=90^o-14^o`

`2x=76^o`

`x=38^o`