Question

The 2nd largest hailstone every measured fell in Aurora, Nebraska, in 2003. The circumference of that hailstone was 16 inches. Using the circumference and the information below, answer the following questions.

What you need to know:
O Kinetic Energy = 0.5 * Mass * Velocity^2 (Units: Mass ---> kg, Velocity ---> m/s)
O Density of the ice in the hail stones = 29 lbs/ft^3
O The volume of a sphere is (4/3) x π x r^3
O The fall velocity of a hailstone in still air can be approximated using this equation V = k√d where k = 20 if d (the diameter of the stone) is given in centimeters. V will have units of meters per second (m/s) as long as d is in cm.
O Density = Mass/Volume
Questions:
O Assume the hailstone was spherical (it was actually oblate and measured 8 inches across)
1. What was the diameter of the hailstone in inches______ and in cm______ and in feet _______?
2. What was the total volume of the hailstone in cubic inches______ and cubic feet________?
3. What was the fall velocity of this hailstone in m/s_________ and in mph________?

Answer 1

1. What was the diameter of the hailstone in inches_5.09_ and in cm___12.92___ and in feet ____0.42___?

2. What was the total volume of the hailstone in cubic inches___68.64___ and cubic feet____0.03____?

3. What was the fall velocity of this hailstone in m/s_____2.584____ and in mph___5.78_____?

Step-by-step explanation:

1. If the circumference (L) of the stone is 16 inches, then from the following equation

`L = 2\pi R`

`R = (L)/(2\pi) = (16)/(2\pi) = 2.54 ~inches`

`D = 2R = 5.09 ft`

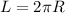
1 inch = 2.54 cm = 0.08 ft, so 5.09 inches = 12..92 cm = 0.42 ft

2. The total volume is

`V = (4)/(3)\pi R^3 = (4)/(3)\pi (2.54)^3 = 68.64~in^3\\68.64 ~in^3 = 0.03~ft^3`

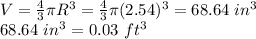
3. The fall velocity is V = kd, where k = 20 if d is in cm. Let's calculate the fall velocity in cm.

`V = 20*12.92 = 258.4~cm/s = 2.584~m/s`

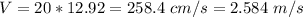
2.584 m/s = 5.78 mph