Step-by-step explanation:
The log formula rearranges an exponential term. I find it helpful to remember that a logarithm is an exponent.
If you start with the exponential term ...
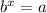
you will notice that the base of it is "b" and the exponent is "x". The log formula rearranges this to ...
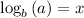
That is, "x" is the power to which the base must be raised in order to give you the value "a".
__
Examples
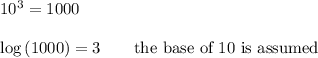
When the base is e ≈ 2.7182818284590..., the logarithm is called the "natural log". Its function name is differentiated from the log base 10 by calling it "ln".
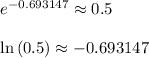
__
You know that multiplication is performed by adding exponents of powers of the same base:

Logarithms work the same way that exponent arithmetic works:

_____
e is an irrational number. One of the possible definitions of it is shown in the attachment.