Question

A random sample of 64 observations produced a mean value of 84 and standard deviation of 5.5. The 90% confidence interval for the population mean μ is between_________.

Answer 1

Answer: The 90% confidence interval for the population mean μ is between 82.85 and 85.15,

Explanation:

When population standard deviation is not given ,The confidence interval population proportion is given by (
`\mu` ):-

`\overline{x}\pm t^*(s)/(√(n))`

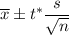
, where n= Sample size.

s= Sample standard deviation

`\overline{x}` = sample mean

t* = Critical t-value (Two-tailed)

As per given , we have

`\overline{x}=84`

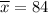
n= 64

Degree of freedom : df = n-1=63

s= 5.5

Significance level :
`\alpha=1-0.90=0.1`

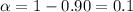
Two-tailed T-value for df = 63 and
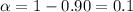`\alpha=1-0.90=0.1` would be

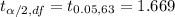`t_(\alpha/2,df)=t_(0.05,63)=1.669` (By t-distribution table)

i.e. t*= 1.669

The 90% confidence interval for the population mean μ would be

`84\pm (1.669)(5.5)/(√(64))`

`=84\pm (1.669)(5.5)/(8)`

`\approx84\pm 1.15`

`=(84-1.15,\ 84+1.15)=(82.85,\ 85.15)`

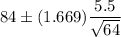
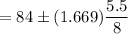
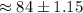
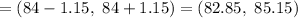
∴ The 90% confidence interval for the population mean μ is between 82.85 and 85.15,