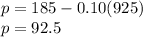Question

If, in a monopoly market, the demand for a product is p = 185 − 0.10x and the revenue function is r = px, where x is the number of units sold, what price will maximize revenue?

Answer 1

The price that'll maximize revenue is
`p=92.5`

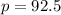
Explanation:

We know that the revenue function is
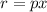`r = px` where x is the number of units sold and p is the demand function given by
`p = 185 - 0.10x`.

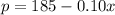Therefore,

`r = px \\r=(185 - 0.10x)x\\r=185x-0.1x^2`

The maximums of a function are detected when the derivative is equal to zero so, to find what value of x maximizes the revenue function, we must find the derivative of the revenue function (
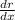`(dr)/(dx)`) and set it equal to 0.

`(d)/(dx) r=(d)/(dx) (185x-0.1x^2)\\\\(d)/(dx) r=(d)/(dx)\left(185x\right)-(d)/(dx)\left(0.1x^2\right)\\\\(d)/(dx) r=185-0.2x`

`185-0.2x=0\\185\cdot \:10-0.2x\cdot \:10=0\cdot \:10\\1850-2x=0\\1850-2x-1850=0-1850\\-2x=-1850\\(-2x)/(-2)=(-1850)/(-2)\\x=925`

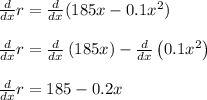
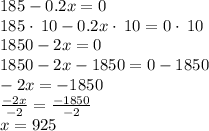
Therefore, the price that'll maximize revenue is

`p = 185 - 0.10(925)\\p=92.5`