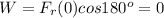Answer:
The normal force is perpendicular to the displacement
The static friction force produces no displacement
Step-by-step explanation:
Work Done By Special Forces
The work is a physical magnitude that measures the dot product of the force applied to an object by the displacement it produces in it.
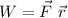
It can be written in its scalar version as
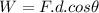
Being F and d the magnitudes of the force and displacement, and
 the angle between them
the angle between them
If the angle is zero, the work is at maximum, it the angle is 90°, the work is zero. If the angle is between 90° and 180°, the work is negative.
The normal force acts in the vertical direction when the object is being pushed horizontally. It means the angle between the force and the displacement is 90°, thus the work is
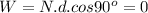
The work is zero because the force and the displacement are perpendicular
The static friction force exists only when the object is being applied a force of a magnitude not large enough to produce movement, i.e. the object is at rest. If the object is moved, the friction force is still present, but it's called dynamic friction force, usually smaller than the static.
Since in this case, there is no displacement, d=0, and the work is