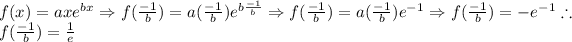Question

Consider the family of functions defined by y=axe^bx, where a and b are nonzero constants with a.0. Find the absolute minimum value of axe^bx of a and c.

Answer 1

`f((-1)/(b))=(1)/(e)`

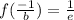
Explanation:

1) According to Fermat Theorem, local extrema can only occur at critical points. So let's evaluate the 1st derivative of that function to find a critical point, that in case of f'(c)=0 a critical point may be a local extrema.

`y=axe^(bx)\\\frac{\mathrm{d} }{\mathrm{d} x}[axe^(bx)]\Rightarrow y'=a(xe^(bx))'+(a)'xe^(bx)\Rightarrow y'=\left(abx+a\right)\mathrm{e}^(bx)\\\left(bx+1\right)\mathrm{ae}^(bx)=0\Rightarrow x=(-1)/(b)\\`

2) Plugging in the point
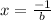`x=(-1)/(b)` in the function, for nonzero a and b to find the absolute minimum value of that function:

`f(x)=axe^(bx)\Rightarrow f((-1)/(b))=a((-1)/(b))e^{b(-1)/(b)}\Rightarrow f((-1)/(b))=a((-1)/(b))e^(-1)\Rightarrow f((-1)/(b))=-e^(-1)\therefore f((-1)/(b))=(1)/(e)`