Answer:
About the x axis
![V = 4\pi[ (x^5)/(5)] \Big|_0^2 =4\pi *(32)/(5)= (128 \pi)/(5)](https://img.qammunity.org/2021/formulas/mathematics/college/9dc77vo683fezyk6awd7sz6saxr2ib12qk.png)
About the y axis
![V = \pi [4y -y^2 +(y^3)/(12)] \Big|_0^8 =\pi *(32)/(3)= (32 \pi)/(3)](https://img.qammunity.org/2021/formulas/mathematics/college/dsh0zl8d4geomnehcj89oc6hi3i5al93xv.png)
About the line y=8
![V = \pi [64x -(32)/(3)x^3 +(4)/(5)x^5] \Big|_0^2 =\pi *(128-(256)/(3) +(128)/(5))= (1024 \pi)/(5)](https://img.qammunity.org/2021/formulas/mathematics/college/6c8us12vfpduszyhyzxh9i0wp0dz548rm7.png)
About the line x=2
![V = (\pi)/(2) [(y^2)/(2)] \Big|_0^8 =(\pi)/(4) *(64)= 16\pi](https://img.qammunity.org/2021/formulas/mathematics/college/6kc74j3elv8e603uxryrf4jgwwzxh54ikm.png)
Explanation:
For this case we have the following functions:
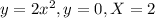
About the x axis
Our zone of interest is on the figure attached, we see that the limit son x are from 0 to 2 and on y from 0 to 8.
We can find the area like this:
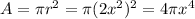
And we can find the volume with this formula:
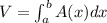
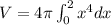
![V = 4\pi [(x^5)/(5)] \Big|_0^2 =4\pi *(32)/(5)= (128 \pi)/(5)](https://img.qammunity.org/2021/formulas/mathematics/college/g5j6yy504x9mzw3ma8933pjw2l9gq7f0qd.png)
About the y axis
For this case we need to find the function in terms of x like this:
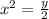
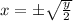 but on this case we are just interested on the + part
but on this case we are just interested on the + part
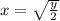 as we can see on the second figure attached.
as we can see on the second figure attached.
We can find the area like this:
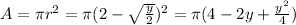
And we can find the volume with this formula:
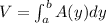

![V = \pi [4y -y^2 +(y^3)/(12)] \Big|_0^8 =\pi *(32)/(3)= (32 \pi)/(3)](https://img.qammunity.org/2021/formulas/mathematics/college/dsh0zl8d4geomnehcj89oc6hi3i5al93xv.png)
About the line y=8
The figure 3 attached show the radius. We can find the area like this:
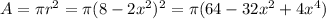
And we can find the volume with this formula:
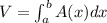
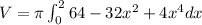
![V = \pi [64x -(32)/(3)x^3 +(4)/(5)x^5] \Big|_0^2 =\pi *(128-(256)/(3) +(128)/(5))= (1024 \pi)/(5)](https://img.qammunity.org/2021/formulas/mathematics/college/6c8us12vfpduszyhyzxh9i0wp0dz548rm7.png)
About the line x=2
The figure 4 attached show the radius. We can find the area like this:
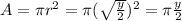
And we can find the volume with this formula:
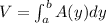

![V = (\pi)/(2) [(y^2)/(2)] \Big|_0^8 =(\pi)/(4) *(64)= 16\pi](https://img.qammunity.org/2021/formulas/mathematics/college/6kc74j3elv8e603uxryrf4jgwwzxh54ikm.png)