Answer:
(D) 9.893
Explanation:
Given:
The equation to solve is given as:
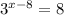
Since, the variable 'x' is in the exponent, we take log on both the sides.
Taking log to base 3 on both the sides, we get:
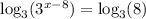
Using logarithmic property
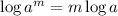
Therefore, the left hand side of the equation becomes;
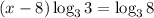
We know that,
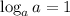
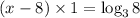
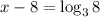
Now, using the change of base property of log
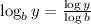 , we get:
, we get:
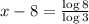
Adding 8 on both sides, we get:
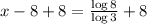
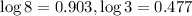

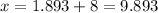
Hence, option D is correct.