Question

Solve 3x − 8 = 8 for x using the change of base formula log base b of y equals log y over log b.

−7.472
−6.107
8.528
9.893

Answer 1

9.893

Explanation:

this is for flvs students I just took the test

Answer 2

(D) 9.893

Explanation:

Given:

The equation to solve is given as:

`3^(x-8)=8`

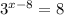
Since, the variable 'x' is in the exponent, we take log on both the sides.

Taking log to base 3 on both the sides, we get:

`\log_3 (3^(x-8))=\log_3 (8)`

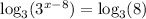
Using logarithmic property
`\log a^m=m\log a`

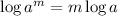
Therefore, the left hand side of the equation becomes;

`(x-8)\log_3 3=\log_3 8`

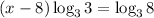
We know that,
`\log_a a=1`

`(x-8)* 1=\log_3 8`

`x-8=\log_3 8`

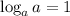
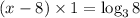
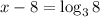
Now, using the change of base property of log
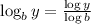`\log_b y=(\log y)/(\log b)`, we get:

`x-8=(\log 8)/(\log 3)`

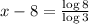
Adding 8 on both sides, we get:

`x-8+8=(\log 8)/(\log 3)+8`

`\log 8 = 0.903, \log 3 = 0.477`

`x= (0.903)/(0.477)+8`

`x=1.893+8=9.893`

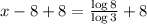
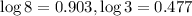
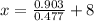
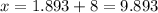
Hence, option D is correct.