Question

A proposed space elevator would consist of a cable stretching from the earth's surface to a satellite, orbiting far in space, that would keep the cable taut. A motorized climber could slowly carry rockets to the top, where they could be launched away from the earth using much less energy.What would be the escape speed for a craft launched from a space elevator at a height of 56,000 km? Ignore the earth's rotation.

Answer 1

To solve this problem we will apply the concepts related to energy conservation. Here we will use the conservation between the potential gravitational energy and the kinetic energy to determine the velocity of this escape. The gravitational potential energy can be expressed as,

`PE= (GMm)/(d)`

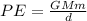
The kinetic energy can be written as,

`KE= (1)/(2) mv^2`

Where,

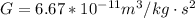`G = 6.67*10^(-11)m^3/kg\cdot s^2`Gravitational Universal Constant

`m = 5.972*10^(24)kg` Mass of Earth

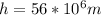`h = 56*10^6m` Height

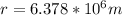`r = 6.378*10^6m` Radius of Earth

From the conservation of energy:

`(1)/(2) mv^2 = (GMm)/(d)`

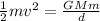
Rearranging to find the velocity,

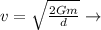`v = \sqrt{(2Gm)/(d)} \rightarrow` Escape velocity at a certain height from the earth

If the height of the satellite from the earth is h, then the total distance would be the radius of the earth and the eight,

`d = r+h`

`v = \sqrt{(2Gm)/(r+h)}`

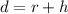
Replacing the values we have that

`v = (2(6.67*10^(-11))(5.972*10^(24)))/(6.378*10^6+56*10^6)`

`v = 3.6km/s`

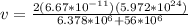
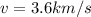
Therefore the escape velocity is 3.6km/s