Question

The truck travels in a circular path having a radius of 50 m at a speed of v = 4 m>s. For a short distance from s = 0, its speed is increased by v # = (0.05s) m>s 2, where s is in meters. Determine its speed and the magnitude of its acceleration when it has moved s = 10 m.

Answer 1

Magnitude of velocity when s is 10 m= 4.58m/s

Magnitude of acceleration when s is 10 m = 0.653 m/s²

Step-by-step explanation:

Radius of circular path = 50m

Speed = 4m/s

increase in acceleration = (0.05s)m/s²

speed and acceleration when s is 10 m = ?

Magnitude of Velocity:

From third equation of motion

`v_(f)^(2)-v_(i)^(2)=2aS\\\\v_(f)=\sqrt{2aS+v_(i)^(2)} \\\\v_(f)=\sqrt{2(0.05)(10)+(4)^(2)} \\\\v_(f)=4.58\,m/s`

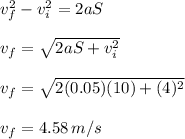
Magnitude of Acceleration:

`a=\sqrt{a_(t)^(2)+a_(n)^(2)}--(1)`

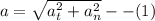
The tangential component of acceleration is

`a_(t)=(0.05)(10)\\a_(t)=0.5\,m/s^(2)`

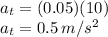
The normal component of acceleration is

`a_(n)=(v^(2))/(R)\\\\a_(n)=(16)/(50)\\\\a_(n)=0.42\,m/s^(2)`

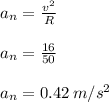
Substituting tangential and normal component in (1)

`a=\sqrt{(0.5)^(2) +(0.42)^(2) }`

a=0.653 m/s²