Question

A disk, with a radius of 0.30 m, is to be rotated like a merry-go-round through 800 rad, starting from rest, gaining angular speed at the constant rate α1 through the first 400 rad and then losing angular speed at the constant rate α1 until it is again at rest. The magnitude of the centripetal acceleration of any portion of the disk is not to exceed 405 m/s2. (a) What is the least time required for the rotation? (b) What is the corresponding value of α1?

Answer 1

(A) 43.55 s

(B) 1.69 rad/s^{2}

Step-by-step explanation:

radius (r) = 0.3 m

rotating trough (θ) = 800 rad

initial angular speed (ω°) = 0

maximum centripetal acceleration (α) = 405 m/s^{2}

rate of speed gain = α1

rate of speed loos = α1

(A) we fist have to get the maximum angular speed from the equation below.

maximum centripetal acceleration (α) =
`(w^(2))/(r)`

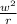
where ω = maximum angular speed

405 =
`(w^(2))/(r)`

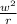
ω =
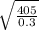`\sqrt{(405)/(0.3) }` = 36.74 rad/s

from the equation of angular motion for constant angular acceleration

θ=
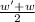`(w'+w)/(2)` x t we can get the time taken to attain maximum speed

where

• ω' = initial angular speed = 0
• ω = maximum angular speed = 36.74 rad/s
• t = time

400 =
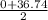`(0+36.74)/(2)` x t

t = (400 x 2) / 36.74

time taken to attain maximum speed (t) = 21.77 s

since the disk gains speed at the same constant rate as it looses it, the time taken to attain the maximum speed is equal to the time taken to decelerate back to rest, the total time = 2 x time taken to attain maximum speed (t)

total time = 2 x 21.77 = 43.55 s

(B) from the equation of angular motion for constant angular acceleration

ω= ω' + α1 x t

36.74 = 0 + ( α1 x 21.77)

α1 = 36.74 /21.77 = 1.69 rad/s^{2}