Question

A 2mC charge traveling 10 m/s nears a wire carrying a 5 A current. If the charge's velocity and the wire's current are perpendicular when they are 1 cm apart, what is the magnetic force on the wire at that moment?

Answer 1

F = 0.

Step-by-step explanation:

The relation between a moving charge and the force on that charge exerted by the current carrying wire is

`d\vec{F} = Id\vec{l}*\vec{B}`

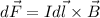
where B is the magnetic field produced by the moving charge.

`\vec{B} = (\mu_0)/(4\pi)\frac{q\vec{v} * \^r}{r^2}`

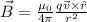
Here, attention must be given to the cross product. If the velocity of the charge is perpendicular to the current in the wire, then the cross product v x r is equal to zero, which makes the magnetic field equal to zero.

If the magnetic field on the wire is equal to zero then, the net magnetic force on the wire is equal to zero.

A common mistake in these questions is to avoid the fact that the force on the wire depends on the magnetic field produced by another source. The magnetic field produced by the wire itself cannot apply a force on itself. It can only apply a force on the moving charge. But in this question, the force on the wire is asked. So it is zero.

Answer 2

To solve this problem we will apply two concepts that are mutually intertwined and are the Law of Ampere and the Lorentz Force. By the law of Ampere we can define the magnetic field and by the law of Lorentz the Force.

The magnetic field at a given point at a current of 5A can be found under the function

`B = (\mu_0 I)/(2\pi r)`

Here,

`\mu_0 =` Permeability constant

I = Current

r = Distance

`B = ((4*10^(-7))(5))/(2*10^(-2))`

`B = 1*10^(-4)T`

Now the charge is given as 2mC and in the Lorentz equation we have that

F = qvB

Where,

q = Charge

v = Velocity

B = Magnetic Field,

Then replacing,

`F = qvB`

`F = 2*10^(-3)*10*10^(-4)`

`F = 2*10^(-6)N`

Therefore he magnetic force on the wire at that moment is
`2*10^(-6)N`