Answer:
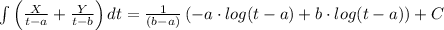
Step-by-step explanation:
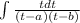 (1)
(1)
We can use partial fraction to solve this kind of integral.
In partial fraction we need to split the this fraction in two new fractions:
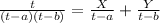 (2)
(2)
Now, we need to find the values of X and Y.
Let's work the right equation of (2). We can use least common denominator
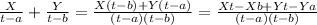
Now we can use common factor in the numerator.
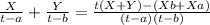 (3)
(3)
If we see, we can compere the (3) whit the left side of (2).
The numerators are the same, so we can compare term by term, like this:
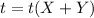 (4)
(4)
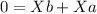 (5)
(5)
We just need to solve the system of equations ((4) and (5)) to find X and Y.
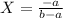 and
and
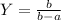
Now, putting this two values in (2) and next we will take the integral.
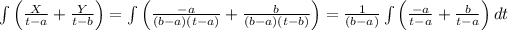
Let's recall that the integral of (1/(x-a))dx is log(x-a), so using it we can find the integral.
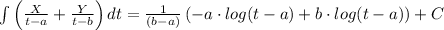
I hope it helps you!