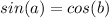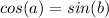Question

In triangle abc angle a +angle b =90 then sin a =

Answer 1

`sin(a)=cos(b)`

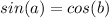
Explanation:

we know that

In the triangle abc

if
`m\angle a+m\angle b=90^o`

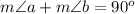
then

`m\angle c=90^o`

Because, the sum of the interior angles in a triangle must be equal to 180 degrees

therefore

Triangle abc is a right triangle

see the attached figure to better understand the problem

The sine of angle a is equal to divide the opposite side to angle a by the hypotenuse

so

`sin(a)=(x)/(z)`

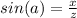
The cosine of angle b is equal to divide the adjacent side to angle b by the hypotenuse

so

`cos(b)=(x)/(z)`

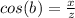
therefore

`sin(a)=cos(b)`

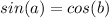
When two angles are complementary, the sine of one angle is equal to the cosine of the other angle and the cosine of one angle is equal to the sine of the other angle

so

`sin(a)=cos(b)`

`cos(a)=sin(b)`