Question

During practice, a softball pitcher throws a ball whose height can be modeled by the equation h = -16t^2 + 24t +1, where h = height in feet and t = time in seconds. How long does it take for the ball to reach a height of 6 feet?

Answer 1

t = 0.25 seconds

It takes 0.25 seconds for the ball to reach a height of 6 ft after the pitcher throws it.

Explanation:

the height is given as function of time. h(t).

`h(t) = -16t^2 + 24t +1`

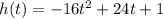
to find the time it takes for the ball to reach the height of 6 feet. It means that we're already told that h(t) = 6. and now we only need to solve for t.

`h(t) = 6`

`6 = -16t^2 + 24t +1`

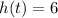
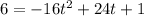
now solve for t. Move everything to the left side of the equation so that highest power term is positive (it just looks cleaner that way, no other reason for doing this)

`16t^2-24t -1+6=0`

`16t^2-24t +5=0`

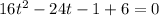
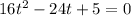
we have a quadratic equation, there are many ways to solve this. But we'll use the quadratic formula:

`t = (-b\pm √(b^2 - 4ac))/(2a)`

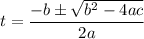
here a = 16, b = -24 and c = 5

`t = (-(-24)\pm √(((-24)^2 - 4(16)(5)))/(2(16))`

`t = (24\pm √((256)))/(32)`

`t = (24 + 16)/(32)\, ,\,(24 - 16)/(32)`

`t = 1.25\, ,\,0.25`

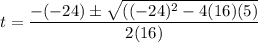
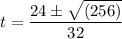
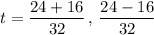
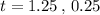
now we have two values for time. But we need to think about which value to select.

The ball first goes upward and reaches a height of 6 ft, then after reaching its maximum height it falls down and again falls to a height of 6 ft.

so the earlier time is what we should select, since we need to find how long the ball takes to reach the height of 6 ft after the pitcher throws it.

So, the correct answer t = 0.25 seconds

It takes 0.25 seconds for the ball to reach a height of 6 ft after the pitcher throws it.