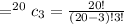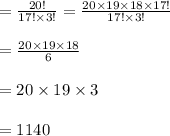Answer:
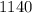
Explanation:
Combinations : If we want to choose
 items out of
items out of
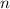 items, and order of the selection does not matter.
items, and order of the selection does not matter.
possible ways
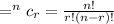
Total number of students
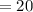
Persons in subcommittee
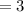
Here order of selection does not matter, so we can use combination to get possible number of ways.
Number of ways