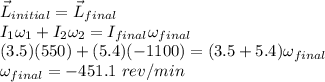Question

Two disks are mounted (like a merry-go-round) on low-friction bearings on the same axle and can be brought together so that they couple and rotate as one unit. The first disk, with rotational inertia 3.5 kg·m2 about its central axis, is set spinning counterclockwise at 550 rev/min. The second disk, with rotational inertia 5.4 kg·m2 about its central axis, is set spinning counterclockwise at 1100 rev/min. They then couple together.

(a) What is their angular speed (rev/min) after coupling?
(b) If instead the second disk is set spinning clockwise at 1100 rev/min, what is their angular velocity (in rev/min, using the correct sign for direction) after they couple together?

Answer 1

(a) 883.7 rev/min to the counterclockwise direction.

(b) 451.1 rev/min to the clockwise direction.

Step-by-step explanation:

(a) The conservation of angular momentum should be used to solve this question.

Keep in mind that the moment of inertia of the combined objects are the sum of the moment of inertia of the objects separately.

`\vec{L}_(initial) = \vec{L}_(final) \\I_1\omega_1 + I_2\omega_2 = I_(final) \omega_(final)\\(3.5)(550) + (5.4)(1100) = (3.5 + 5.4)\omega_(final)\\\omega_(final) = 883.7~rev/min`

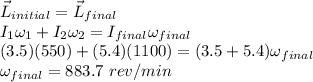
(b) By the conservation of angular momentum:

`\vec{L}_(initial) = \vec{L}_(final)\\I_1\omega_1 + I_2\omega_2 = I_(final)\omega_(final)\\(3.5)(550) + (5.4)(-1100) = (3.5 + 5.4)\omega_(final)\\\omega_(final) = -451.1~rev/min`