Answer:
7.37 is the pH of the buffer.
Step-by-step explanation:
To calculate the pH of acidic buffer, we use the equation given by Henderson Hasselbalch:
![pH=pK_a+\log(([salt])/([acid]))](https://img.qammunity.org/2021/formulas/biology/college/6usxe642bp3w274zbcv30her0kcessu95f.png)
![pH=pK_a+\log(([Na_2HPO_4])/([NaH_2PO_4]))](https://img.qammunity.org/2021/formulas/biology/college/mdqmk78xb6spu6slfsnnubkr14dymvjxa7.png)
We are given:
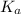 = dissociation constant =
= dissociation constant =
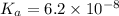
Moles of
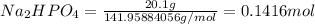
Moles of
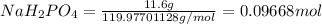
![[concentration]=(moles)/(volume (L))](https://img.qammunity.org/2021/formulas/biology/college/4gwwdduakkoe8dg8usclpyarvbxgkdappt.png)
![[NaH_2PO_4]=(0.09668 mol)/(1 L)=0.09668 M](https://img.qammunity.org/2021/formulas/biology/college/1djn118nvfq1ja7axgltbx504t0z46ebc6.png) (acid)
(acid)
![[Na_2HPO_4]=(0.1416 mol)/(1 L)=0.1416 M](https://img.qammunity.org/2021/formulas/biology/college/u0yraq4rwdht585zmzm3izs9laa9n49y0t.png) (salt)
(salt)
pH = ?
Putting values in above equation, we get:
![pH=-\log[6.2* 10^(-8)]+\log((0.1416 M)/(0.09668 M))\\\\pH=7.37](https://img.qammunity.org/2021/formulas/biology/college/93n9saijq6vl7nd8lrhf44say6zhgghsj5.png)
7.37 is the pH of the buffer.