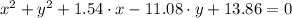Question

Find an equation of the circle that passes through points (6,3) and (-4,-3) and has its center on line y-2x-7.

Answer 1

`x^2+y^2+1.54\cdot{x}-11.08\cdot{y}+13.86=0`

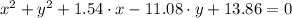
Explanation:

We can use the general formula method:

`x^2+y^2+2\cdot(g)\cdot{x}+2\cdot(f)\cdot{y}+c=0`

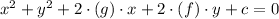
We substitute point 1 (6,3) into the equation:

`6^2+3^2+12\cdot(g)+6\cdot(f)+c=0`

`12\cdot(g)+6\cdot(f)+c=-45`

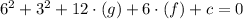
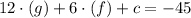
We substitute point 2 into the equation

`(-4)^2+(-3)^2-8\cdot(g)-6\cdot(f)+c=0`

`-8\cdot(g)-6\cdot(f)+c=-25`

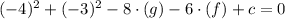
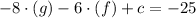
We know that he centre is (-g,-f) and we substitute it into equation y-2x-7=0

`-f+2\cdot{g}-7=0`

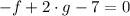
We have 3 equations and we have 3 unknowns. We can eliminate c by subtracting the first two equations:

`20\cdot(g)+12\cdot(f)=-20`

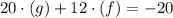
now we can solve in terms of f and g:

`f=2\cdot{g}-7` into the above equation:

`20\cdot(g)+24\cdot{g}-14=-20`

Solve for g:

`g=0.77`

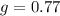
f is
`f=-5.45`

Therefore c is:

`-8\cdot(0.77)-6\cdot(-5.45)+c=-25`

`c=13.86`

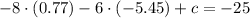
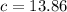
The equation of the circle is:

`x^2+y^2+1.54\cdot{x}-11.08\cdot{y}+13.86=0`