Question

A geochemist measures the concentration of salt dissolved in Lake Parsons and finds a concentration of . The geochemist also measures the concentration of salt in several nearby non-isolated lakes, and finds an average concentration of . Assuming the salt concentration in Lake Parsons before it became isolated was equal to the average salt concentration in nearby non-isolated lakes, calculate the percentage of Lake Parsons which has evaporated since it became isolated. Round each of your answers to significant digits.

Answer 1

Question:

A geochemist measures the concentration of salt dissolved in Lake Parsons, an isolated salt lake. He finds a concentration of 74 gL−1. The geochemist also measures the concentration of salt in several nearby non-isolated lakes, and finds an average concentration of 6.5 gL−1. Assuming the salt concentration in Lake Parsons before it became isolated was equal to the average salt concentration in nearby non-isolated lakes, calculate the percentage of Lake Parsons which has evaporated since it became isolated.

Answer:

The percentage of Lake Parsons evaporated is 91 %

Explanation:

Let us say that Lake Parsons water content initially = X and salt content = Y

Therefore,

`(Y)/(X) = 6.5`

Y = 6.5 X

After Lake Parsons became isolated, its salt content remained unchanged i.e. Y

However, its water content decreased due to evaporation. Suppose now its water content = Z

Therefore we can write

`(Y)/(Z) = 74`

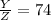
Substituting the Y value

\frac{6.5X}{Z} = 74

`(X)/(Z) = (74)/(6.5)`

`(Z)/(X)= (6.5)/(74)`

`(Z)/(X) = 0.0878`

`(Z)/(X)= 8.78`

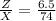
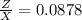
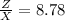
Therefore the Lake Parsons have now 8.78 % of the initial water.

Now the percentage of Lake Parsons evaporated

= (100 - 8.78)

= 91.22

= 91 % (rounding to 2 significant digits)